二重数ってはじめて聞いたけどどんなもの?><; って思ってググったけどおもしろい><
「2乗してはじめて0になる数」とかあったら面白くないですか?ですよね - アジマティクス https://www.ajimatics.com/entry/2021/03/22/174633
二重数ってはじめて聞いたけどどんなもの?><; って思ってググったけどおもしろい><
「2乗してはじめて0になる数」とかあったら面白くないですか?ですよね - アジマティクス https://www.ajimatics.com/entry/2021/03/22/174633
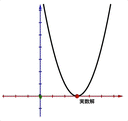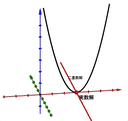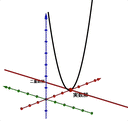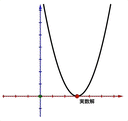
「2乗してはじめて0になる数」とかあったら面白くないですか?ですよね - アジマティクス https://www.ajimatics.com/entry/2021/03/22/174633

もちろん、世界中のあらゆる機械の通知音をamazonが収集してとかすごい話じゃなく、手動でユーザーが各々「これはこの機器の通知」って設定するやつ><
音声認識と比較したらはるかに簡単に出来そうだし、ハードウェアリソース的にはamazon echoみたいなマシンでもローカル処理で出来そうな気がする・・・><
部屋の中で鳴る音を聞き取って、どの機器の何の通知かに変換してLAN内にブロードキャストする仕組みが必要。
コウモリであるとはどのようなことか - Wikipedia
https://ja.wikipedia.org/wiki/%E3%82%B3%E3%82%A6%E3%83%A2%E3%83%AA%E3%81%A7%E3%81%82%E3%82%8B%E3%81%A8%E3%81%AF%E3%81%A9%E3%81%AE%E3%82%88%E3%81%86%E3%81%AA%E3%81%93%E3%81%A8%E3%81%8B

エスパーテックサポート、猫の行動観察やその他の生物の行動、航空機のコクピット哲学や広義のオートメーションの実装、航空機事故時のパイロットの行動、高度なヒューマノイドロボットが実現した場合の適切な振る舞い、さらに言うなら国際情勢での各キーパーソンや集団の行動、
オレンジの趣味的には、オレンジとは違う考えを持つ存在がどう世界を認識してどう判断してるのか?という面への興味として結構共通なものとして見てるかも><
例えば、オレンジは猫の行動観察もすごく好きだけど、なんでかと言うと単に猫がもふもふでかわいいからだけじゃなく、人間とは異なりながらも人間社会にかなり近い位置で生活する猫が、どういう風に物事を捉えてどう判断してどう行動するのかを読み説くのがとても楽しいからで、これは猫や動物に限らずなんらかのプログラムによって動いている計算機によって動いている機械が、どう物事をとらえどう判断しているのか? にも及ぶので、結構広い分野にたいして共通した興味かも><
「疎い人がどういう風に認識しているか?」までが分野内かは難しいけど、「人やなんらかの思考できる存在が物事をどう捉えているか?」についての興味は、たしかにその個別の分野からはちょっと離れてて、認知科学とか脳科学とか行動学とかそっち系っぽいかも・・・><
まあ元も子もない話をしてしまうと、科学分野なんて誤ったことを盲信しているばかりか人々に広めようとしている人々は無限にいるわけで、いちいち相手してらんないですよ
「あなたがXをどう間違っているか」に関心を持っているのは人や人々への関心の為せる業であって、 X そのものへの興味とはちょっとズレていると思う (無関係とも思わないけど)
それは人に関心があるか理屈に関心があるかの違いじゃない?
マインクラフトで自宅を溶岩で燃やしてしまう芸風で、加湿器に水いれなきゃならないって知らなかったり色々ぬけてるVTuberの人の訓練されたベテランリスナーとかは、そういうの慣れてると思うし、いわゆるポンなVTuber全般のベテランリスナーってそういうお節介テックサポートとかが好きな人々っぽいイメージがあるかも・・・というかエスパーテックサポート並みにコメントで言い当ててる事例結構見かけるかも><
オレンジの場合はオレンジが好きな分野を理解していない人オレンジが知ってる範囲の知識を教えながら相手に脳内モデルを読み説くのがとても楽しいので、
もしオレンジが数学大好きで「数学チョットワカル>< 数学わからんやついねーが><」って人でもあったならば、オレンジみたいな『独自の謎の数学モデルを構築し かつ それにほぼ確実に誤りがあるっぽいけどわからんと自覚してる人』を見つけたら、その人の考えを読みといて矛盾の正体を解説したりしながら教えるの、楽しくてしょうがないと思うんだけど><
でも、数学分野が得意なそんなタイプの人に会ったこと無いし、それに近い存在の実例、にじさんじの数学天才VTuberの人くらいなのかも?><
って思うかも><
数学に人生を費したからといって人類の最先端に到達できるわけではないのは既に知られている話で。
結局それは古典物理学で生きていた人々が時空の歪みに気付かなかったのと同じで、我々が対話できる/するつもりのある相手と、教えられる/教われるレベルの事柄と、その両方が揃っている場合しか見ていないだけではと。
相手が理解する気でいて、やる気と体力と時間が十分にある場合に、一対一で教える側が十分なコストを支払えば、物事を十分なレベルまで「教える」ことができるだろうというくらいのところはまあ気持ちはわかるんだけど、それが有限時間で終わるとは限らないと私は思っているよ
それは (言葉は悪いけど) 最底辺に揃えるならばという話ですよね。
私としては、「ある程度の説明でちゃんと基礎を習得できる人々がいて、そういった人々はさっさと先に進めばいいし、そうでなかった人々はじっくりやればいい」という考えなので、全員が暗記教育でどうにかするしかないという考えにはむしろ反対です
本題に近い話で言うならば、雑に言うとオレンジはどっちかと言うと「だから妥協して暗記教育にするしかない><」みたいな話をしてたんだけど・・・・><
「一対一で際限なくコストをかければ」という前提での言説を「税金と限りある教員リソースで子供全員を教育する」という場面について持ってくるのは明らかにフェアではないし建設的でない
コスト度外視するのであれば、それは一対一でコンサルする分には好きに一生懸命教えればいいと思うけど、学校教育に持ち込める話ではないですよね。
これを誤謬ではなく「コストをかけていないからだ」の思っているという主張であるとの理解をしています
「物事を正しく理解している人は万人が理解可能な平易な説明をできる」ってTwitterでよく見る誤謬じゃん
This account is not set to public on notestock.
短く言うと「他人に教えられないような物事は理解しているとは言えない><」
と考えているし、オレンジが教えたがりでエスパーテックサポートを好んで行うのも、自分の理解度を測ったり知識の穴を見つけ出したり知識の再構築をするため><
相手が前提知識を持っていようがいまいが誤った理解をしてしまっていようが、しっかり理解しているならばせつめい出来るはずというのは、にじさんじの数学の天才VTuberの人がやってる実例でもあるし、
数学以外では、オレンジがプログラミング出来ない人に教えたり、相手の脳内モデルを探ってメカ音痴の人にエスパーテックサポートするのも同じようなもので『自分が理解している物事について、相手がどう誤った理解をしてしまっているのか読みとければ、その誤りを訂正する説明は出来る』と考えてる><
命名が馬鹿っぽいのは寒いなか超高速で考えて試行錯誤で書いたコードが動いた時点そのままなのであれです><;(言い訳)
オレンジがsqrt計算するアルゴリズムを自作しようとして結局ニュートン法を再発明したっぽい気がする実験コード><
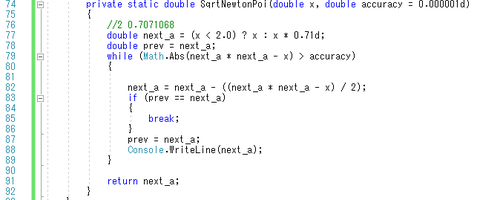
sqrtは逆算できるわけだから正当性(?)や誤りはわりと簡単に見れるかも?><
その日はすごく寒かったから「出来たっぽい!><」でちょっと試してお布団に帰ったので、かっちりしたテストはしてないので無限ループになったりとか愉快なことが起きる可能性もあるけど><
じゃあちょっと文脈が戻りますが、そのどうやらおかしいらしいモデルに基いて導出された「sqrt の計算方法」と思しきものの正当性はどうやって示されるのかというのと、「そもそも間違っている (あるいはその可能性のある) 前提から導出された結果について “理解している” ことを主張するのは有意義なことなのか」という素朴な疑問があってですね。
オレンジは実際に矛盾があると言ってるしどうやらおかしいっぽいと思ってるし、どうおかしいのかについても好奇心が向くので、標準的な数学ではどうなっててオレンジ脳内モデルはどのようにおかしいのかにも強く興味がある><
別に高校数学で学ぶような範囲の数学に誤りがあってオレンジ脳内モデルの方が正しいなんて言ってない><
「オレンジ脳内モデルがどうおかしいのか?><」に興味がある><
まあこれも拗らせると「俺以外の世界全てが間違っている」とか「世界で俺だけが狂っている」とかになるわけで、まあこわいわね
まあ心配を始めるとキリがなくて「私の脳内では論理的に整合していると思っていることが、実は私の脳がサイレントに狂っているだけで実際には整合していない」という可能性に常に怯えて生きていたりするわけで
「実数とは異なる」はまず実数が定義されていないと判定できないし、「ブラックホールのような性質」は具体的に記述されるべきだし
で、『無限小』とゼロ以外の数値の隙間は、『次元』(オレンジなりの概念で適切な単語が他に見つからない><)をひとつあげると見えて、その『次元』上ではその『次元』における『無限小』が見える
みたいなモデルになってる><
sqrtを計算するアルゴリズムを再発明した時も、この『次元』をひとつ上げてから戻すって発想で思い至ったので、もしかしたらオレンジの謎の『次元』って概念が、微積分の代用になってるのかもしれないけどわからない><(?)
よくわかんないけど、オレンジの脳内数値空間上の『無限小』の定義を書けという意味であれば、「ゼロとゼロ以外の実数の隙間にある、実数とは異なるブラックホールのような性質を持つ特殊な数値」かも><
本来これは自然言語でも言えるんだけど、とにかく定義が情報共有の試みで最初のフェーズなので、いいから定義してください
オレンジは四六時中いろんな事をごちゃごちゃ考えていて、オレンジの脳内数値空間も矛盾についても「どうして矛盾が生じるのか?><」とかごちゃごちゃ常に考えてて、つまり未完成なものというか、理解のために考え続けるものみたいになってるかも><
オレンジ脳内数値形式ができてしまってるの文脈の「できてしまってる」は「既存の数学をまるごと置き換える事ができる完全な代用品が!」じゃなくて、「オレンジが今まで数学的な課題(9割くらいがプログラミング関連)を必要に応じてこなす為に実用上編み出された脳内の形式がある」って事><
それには『無限小』が存在したり、なんていっていいかわからないけど人に言う時には『次元』という言葉で説明する概念があって、実用上はそれらに頼っているので、それらを使わないのであれば、代わりにちゃんとした数学上の純正な(?)相当品が必要になるかも><
形式的に記述できないということは「できてしまって」いないということに過ぎないので。
ぶっちゃけ言ってしまうと「できてしまっている」が本当に「できている」なら形式的に記述できるはずなので、さっさとまとめて人に問うなりした方がいいんじゃないのかなと思います。
オレンジが数学に限らず学校の授業が苦手で独学偏重なのも、こういう風に「こうです」で済まされるの耐えられなくて、時間がかかっても自分で納得いくまで深堀しないと気が済まないのがあれかも><
そういうレベルの話じゃなくて、「そもそも自分で記述できないことを問うたって答える側も厳密に議論できるわけないだろ」 (つまり自分で厳密化できない問をあたかも問として成立しているかのように例示してどうすんねん) という話です
オレンジの場合の実数の理解って、オレンジは既に独特な数値空間ができてしまっているわけで、オレンジ数値空間がどうおかしくて、実数はどう便利で、実数はどういう風に成り立ってて、逆に実数で解くには困難がある分野がどうあって、なぜ実数以外の数値空間が発明されてそれはなにがどう違うのか?
みたいな事等々を全部理解していくのが実数の『理解』であって「よくわからんけどそういうものらしい・・・><」は理解したとは言わないかも><
オレンジは実数を理解していないし、
「言葉の定義的にどれの事?」 にたいしての「これの><」であるし、オレンジは実数を完全に理解できていないので知識の結構な部分が暗記で、一部を自分で考えてみて「たしかにオレンジの発想では矛盾するかも><;」みたいに理解していってる程度だし、
「暗記じゃねーか」って「理解してない><」って言ってるんだからそりゃそう><
「そのままこれ」と出してくるのは暗記じゃないんですか?
隙間が無いの隙間ってそのままこれの話かも><
アルキメデスの性質 - Wikipedia https://ja.wikipedia.org/wiki/%E3%82%A2%E3%83%AB%E3%82%AD%E3%83%A1%E3%83%87%E3%82%B9%E3%81%AE%E6%80%A7%E8%B3%AA

その「隙間」という言葉、ちゃんと定義できてます?
定義できるなら論理式みたいに記号的に表現できますよね
無限小という単語を使わずとも、例えば「実数にゼロとゼロ以外の実数の間にも隙間が無いのはなぜか?」を説明できれば、無限小が存在しない事を示せるし、世の中の数学好きな人が何人も「そこにも隙間が無い理由」を説明する文章を書いてるかも><
実数の性質を高校数学程度でも理解できているのであれば、その説明も可能なのでは?><
オレンジは無限小というものがゼロとゼロ以外の実数の隙間にあるという脳内数値空間で考えていたあとに、実数という空間には「そこにも隙間が無い」という事を色々読んで学んだので、なんでそこに隙間があるとマズい事になるのかを部分的には理解したので部分的には説明できるかも><
無限小を定義せずに「ないのはどうしてか?」を問うのってナンセンスなので、まず無限小を定義しないといけないですよね、問う側が。
私の立場としては「値を計算可能、あるいは計算方法を発明可能であることは必ずしも “理解” を測るバロメータとして適切でない」という立場なので。
「理解しなくていい」という https://mstdn.nere9.help/@orange_in_space/107643031774379456 こんな話はしてない
計算可能ではない場合の具体例思いつかないけど、オレンジが無限小を例に出したように、「実数に無限小が無いのはどうしてか?」は、実数をある程度『理解』しているのであれば他人に自分の言葉で説明で来るのでは?><
つまり自分の言葉で他人に説明でき疑問に答えられるというのも試験のようなものとして使えるのでは?><
具体的に「計算可能な値の場合は計算可能であること」とだけ言われても、それに納得するかを別として「じゃあ計算可能でない概念の場合は?」となるわけですよ。最初から generic な話をしてほしい
「そのくらい」のラインがどこにあるかを具体的に知りたいわけではなくて、「そのくらい」のラインがどのような理由や要請や妥当性をもってそこに引かれたのかを知りたいです
本質が計算方法って言いたい訳じゃなく、「本当に理解しているならそのくらいできるでしょ?><」って試験みたいな感じ><
もう一度言うんですが、物事の本質が最終的に「計算方法」に帰着するという世界観の妥当性自体がまず自明ではないです
インターネットミームでいうと
任意の数学の分野や対象、とりあえず例として文章上 円周率を使って示すと、
「円周率を計算するアルゴリズムを再発明出来ない程度の理解は『円周率チョットワカル』であって『円周率完全に理解した』では無いじゃん?><」
って言いたいし、この文章の"円周率"の部分に任意の数学の用語を当て嵌めればオレンジに主張になるかも><
うーん、「ほぼあらゆる人々は何も “理解” していないし “丸暗記” している」という話であれば理解はできるんですが、おおよそナンセンスですね。得られる情報量がほぼ ZERO なので
オレンジの主張としては、計算手法を自ら導ける程度までいかなければ「そういうものだ」で済ませてる部分が残っていて理解出来てるとは言えないと言ってる><
それがある分野や対象で難しいということは、つまりそのままその分野や対象は難しいってことにオレンジの主張上はなるかも><
円周率に固執するからそういうケースが抜けるんじゃないですか
じゃあ私からひとつ疑問を提示したいんですが、「性質をよく知られているナニカについて、それが計算可能であることとその計算手法の両方が簡単に導ける」という暗黙の仮定はどこから来てるんですか?
より低レベルなものであっても理解が必要という一貫性があれば、円周率に関してもどうやったら出せるのかって理解が必要では?><
定数になるのでおkってつまり「誰かがやってくれた事は手抜きしてスルーしよう」ってことになるし、であれば数学の純粋()な理解なんてせずとも、実用的な本にある実用的な式をそのまま目的の数値を当て嵌めて計算器に解かせれば済むのでは?><
つまり、らりおさんの主張は「数学は、必要な公式の丸暗記とその解き方のみ理解すればよく、その成り立ちについて学ぶ必要は無い」と言ってるのと同じでは?><
「どうしてそうのか」という再発明が出来る程度の理解が必要ではなく、単に振る舞いと適用分野のみのより実用的な(計算機用語でいう)高レベルの部分のみが必要だというのであれば、自分が扱う分野、例えばなんらかの工学の分野であればその工学の分野で使用される公式を理解すればいいのであって、なぜそういった公式になるのかの数学的な理解は不要ということになるのでは?><
それって「どういう必要性があってそのような定義を捻出したのか」というある意味メタなレイヤーの話であって (たとえばそうでない定義もできるかもしれない)、具体的な定義対象のことそのものについての理解に直結しているとは限らないと思うんですが
定義に「どうしてそうなるのか」を問う意義をわかっているのかかなり疑問に思っています
その"「円周率の定義を把握している」ことであって、"の把握の事を指してオレンジはルールの『暗記』と言って問題視してる><
それこそ「そういうものだ」であって「どうしてそうなるのか?」では無い><
円周率を “知っている” とするためにまず大事なのは「円周率の定義を把握している」ことであって、そのうえに「円周率が都合よく使える場面をいくらか認識している」などがあるけど、それは円周率を計算できるかどうかとは別の話ですよね
それこそ、さっき例に出した円周率のように
既にまるごと覚えてしまっているアルゴリズム以外で、円周率を計算するアルゴリズムを再発明出来るのであれば、その人が円周率がどういうものであるかを理解しているであろうと観測(?)出来るのでは?><
そうでないのであれば例えば教科書にかかれてる内容を文章としてそのまま覚えそれを述べているにすぎないかもしれない><
(もちろん、実は丸暗記していたアルゴリズムを知らないと嘘をついておいてそれを回答に使うという不正が出来てしまうという穴があるけど><)
再発明ってのはどのくらいの話なんですかね。たとえばある公理系を『再発明』するというのは公理を列挙できればよい? それともそれ以上やそれ以下?
定義のわからない言葉でラベリングされても困るんですが
だからその「暗記」とは何なのかを説明してほしいんですが……
三つ目の論点として、円周率が正しいことを (その性質を利用して) 検証するのと、円周率そのものを導出するのは、問題としての難度が全然違いますよね。
たとえば 7194667284607936697938603328569 の最小の素因数を求めるのと、 7194667284607936697938603328569 の最小の素因数が 2031443 であることを検証できることは全然違う。
それってつまり丸暗記した公式をプログラミングに於けるライブラリのように使っていけば便利に使えるって話であって、じゃあ丸暗記すればいいんでは?><;
理解せずとも丸暗記しておけば、その適用する場面での選択という意味に於いてのみの「応用」が必要であって、公式そのものの意味を理解する必要は無いと言えるかも><
で、実際、現在の高校までの数学では微積分なんかも簡略化して式の丸暗記に近い形で教えるっぽいし><
二つ目の論点として、 “たとえば” 円周率は実際のところ具体的な値よりもその性質の方こそが利用されているのであって (具体的な値は計算の過程で発生する定数にすぎない)、その値を求める計算自体に本質的な重要性や価値があるとは限らないですよね。
ということは、円周率がどういうものであるかをアルゴリズムを再発明出来るほどに理解せずに「3.14くらいらしい。これを掛けると円周出せる」と暗記すれば十分という意味では?><
まず一つ目の論点として、「円周率を求めるひとつの方法を再発明できたとして、そこに基礎としてどれだけの価値があるか?」という話がある。
その方法が円周率の値を求めること以外に応用できないのであれば、可能な知的行動の範囲は円周率の値を最初から知っている場合と大差なくないですか?
円周率がどういったものでありどういう性質のものであるかを理解しているのであれば、それを求めるなんらかのアルゴリズムも再発明出来るのでは?><
そうでないのであれば「よくわかんないけど紐とかで測ったら3倍ちょっとっぽい。なんでかはわからん」でわからんのでは?><
基礎の部分を暗記するうえで「応用」が利くかというのは割と重要な基準で (というか応用できてこその基礎なので)、じゃあ例えばそこで想定される「円周率を求めるアルゴリズム」は円周率以外のさまざまな値を求めるために応用可能なんですか? という基準が抜けている。
例えば例えば、円周率を3.14で暗記しておいて使ってたりプログラミング環境に用意された円周率の定数を使ってる人々のうち、円周率を求めるアルゴリズムをその場で再発明出来る人ってどのくらいの割合だろうとか><
例えば『「無限小の代わりに(というと変だけど)ゼロを使うのはなぜか?」って説明できる人々』と、『そのルールに基づいて計算問題を説く人々』って、それほど人数差がないのかも?><
それを暗記と言うのであれば、その informal な納得の領域というのは言語をはじめあらゆる領域の根底なのであって (人間の知能の bootstrap はそのように行われるので)、そもそも人が「理解」していることがひとつでもあるんですか? と問いたい。
誰も達成しえない空想上の目標を全員に達成させる手段を問うほど虚無なこともないので。
a+1 = b+1 のとき a=b であることを人々は “証明” できないけど、それは informal な形で十分に「納得」できることですよね。
あなたは、人々は、自然数について何を「暗記」しているんですか? と。
そもそもルールをわかってもいないのに「暗記」って何ですか? という話をしています
まあ実数についていうなら、高校程度では実数の特殊な性質のエッジケースを突かない範囲でしか実数を使ってないと思うので
自然数の定義を示せないことと、自然数を適切に扱えることは、話が別でしょう
じゃああなたはそもそも自然数の「定義」や公理系を示せるんですかと。
ということは高校レベルでは「実数とはなにであるか?」ってちゃんと理解しないまま実数というものを使ってるんでは?><
みたいなことが言いたかった><
高校で習う極限と収束まわりは相当ガバガバだし、教師もガバガバであることは明示してくれていた気がする
そもそも無限小の存在の有無ってそのレベルで「習う」話なんです?
オレンジは極端な教えたがりなので、オレンジが知ってる範囲の物事であれば、相手の脳内モデルを読み取って修正するみたいな教えかたするの大好きだし、だからお節介エスパーテックサポートとかしまくってたわけだけど、
そういう人って世の中にあんまりいないだろうし、そういう器質を持っていてなおかつ重度な数学マニアとなるとさらに居ないんでは感><
オレンジが微積分を理解できないの、最小の単位(?)がゼロに近い極限になったり1になったりでわからんというか、この部分は1の方が便利じゃないの?><; みたいな混乱で「なんもわからん><」になってる><
で、難しいし部分的な理解上、部分的であり誤りを含むので矛盾があるままになってて「微積分気持ち悪くて嫌い><」になってる><
この根本的な問題を修正するには、諦めて「そういうものです」系の丸暗記で多大なストレスを受けながら我慢するか、独学の範囲では無理だったオレンジの疑問をひとつひとつ解いてくれる優しい人に習うくらいしかないけど、独自の考えを組み立ててしまった人の脳内モデルの修正は、なにも勉強していないまっ更な人に教えるのと比べ物になら無いほど困難なので、オレンジに教えられる人はたぶん存在しなさそうって思ってる><
オレンジ的に独自脳内数値空間を出したのは、具体的に「世の中の大学入学できるレベルの多数の人は無限小が無い事を既に得ている知識のみで(本を片手にとかググったりとかせずに)人に説明できるのか?><」という疑問がある><
たとえば「古典物理学は厳密には “正確” ではないし、古典物理で説明できないことは存在する (から詳しく知りたくば大学行ってね)」というのと「古典物理を “理解” したうえで正しく説明できる」は両立しますよね
ということは、『高校数学の範囲はしっかりやったけど、大学では数学科に進まなかった かつ 大学の数学科レベルの独学も行わなかった厳密にどうなのか結局わからなかった大多数の人』は、数学を理解の形ではなく暗記の形で覚えてるの言えるのでは?><
と言ってる><
本人に知る気と時間があるならば、教材はそこかしこにあるしどうとでもなりますよ。
知る気がそんなにない人をどうするかなんて、単に経済的な合理性の追究の問題でしかなくない?
じゃあ説明してわかるのか、わかるまで長く厳密な説明をしたところでそれを受け入れられるのか、そのコストを誰が支払うのか、そういう話では?
生徒「なんでそうなるの?」
高校の数学の先生「それは難しい話なので大学の専門分野でやります」
って事は生徒は理解せずに「そういうものだ」と暗記させられるって事でしょ?>< って言いたい><
オレンジが独特な数値の理解で微積分に頼らずに同じようなアルゴリズムを再発明出来てしまったりしているので微積分の必要性をちゃんと理解できないのはあくまで例であって、
高校までの間にそうならないように標準的な数学を『理解』させるのは可能か?><
と言ってる><
(「それは大学の専門分野でやります」って話が多いように見える><)
ま、その結果としてエセ科学にどっぷり浸かったヤバい人が出来上がる可能性も否定できないので、基本的に人におすすめするルートではないけど……自分のことに責任持てるのは自分だけなので
再発明自体は悪いことじゃないし、それに欠陥があると思うなら、自分で考えたモデルなんだから自分の判断で必要なことを学んでいけばいい。高校がどうとか大学がどうとかは関係ない。
そもそも非標準の (欠陥つき) モデルを使っている人が高校レベルとか大学レベルとかのレールを基準に物事を考えているのがよくわからんのですよね
オレンジの疑問をシンプルに言うと「数学の各要素を、再発明できる程度に理解してる人って本当に世の中に多くいるの?><」って事><
高校の数学教育を受けて大学に数学も含めた筆記試験により入学した人のなかで「『無限小』が無い」事をしっかり説明できる人ってどのくらいいるの?><
オレンジみたいな数への理解の誤解というかなんというか独自の(おそらく欠陥がある)数値空間を、数学教育上 標準的な数への理解に矯正するには、それこそ現在高校数学まででやってる範囲では無理なのでは?><(数学好きな人の話を聞く限りでは「それは大学レベルで・・・」って出まくりに感じる><)
となると結局、高校数学までの範囲では現実的に「そういう風に決まってるから納得しろ! 納得いかなければ大学に行ってからやれ」になってしまって、つまり「そういう決まり」の暗記になってしまうんでは?><
オレンジの理解がおかしいというか発想がおかしい点は、オレンジの脳内数値空間が厳密に実数ではなく
「実数(のようなもの)の空間で見ると実数には隙間や誤差は存在しないが、次元をひとつ上げて客観的に俯瞰すると、その空間上では元の次元には隙間や誤差が存在する、そしてその空間はさらに次元をあげると同様に・・・」
って発想で考えて、次元を上げたり下げたり(膨らませたり縮めたり)って、考えてる><
フラクタル図形の隙間みたいな感じ><
暫定的な数値を出して逆算して求めたい答えに近づけるんであれば、求めたい答えとのズレの半分ずつ暫定的な数値を近づけていけば、だんだん近づいていくだろう><
とだけ考えた><
オレンジは微積分の知識使わずにニュートン法もどき(?)を再発明したので、逆に(?)どうしてそれに微積分の知識が必要なのかがさっぱりわからなかった><
で、ニュートン法くらいなら高校レベルの微積を習得していれば簡単に習得できるんじゃないですかね。しらんけど。
ニュートン法とかで x^2-a = 0 を解いた法が圧倒的に楽。機械にやらせるならルンゲクッタ法にしてもいいし
平方根の手計算、開平法が知られがちだけど厳密解が欲しいのでもなければそうはしないやろという感じがある (唐突)
ちなみにオレンジは微積分は全く習ってないし、微積分は表面的な知識のみ見ていて納得がいってない部分があるので理解できてないみたいな状態><
(ので、理解して意識して実用したことはないし、工学の場面で「積分したのでこうなります」みたいな話も「積分がなにか理解してないけど、実際に算出してあってるし、結局お手本の式と同じになったっぽいのであってるっぽい>< 結局積分の意味わからん><」みたいになる><)
オレンジがこの前sqrt(x)を解くの再発明したけど、高校数学を学んだ人ってそれが出来るように教育されてるのかも?><
This account is not set to public on notestock.
「まあ無理でしょ」を reject するなら、「少なくとも留年制度は必要でしょ」が私なりの現時点の見解です
なるほど><
というか、つまり、数学の各項目を「再発明できる程度に理解しろ」ってことなんだと思うし考えは素晴らしいと思うんだけど、にじさんじの数学の天才なVTuberさんが、頭悪い系VTuberさんに数学や算数を教えてるようなしっかりどうしてそうなるのか教えるやり方で教えなきゃならないってことだろうけど、学校教育で現実的に可能なの?><
(「無理でしょでは無く」数学苦手なのでマジでわからない><)
それって「存在を知ってる」であって「わかってる」じゃないので、それで解けない試験問題は大正解では?
オレンジが言う数学での「暗記できない><;」って、例えば(例として実際には覚えてる物で説明すると)
「これはピタゴラスの定理で解ける!><」まではわかっても「・・・・ピタゴラスの定理ってどういう式だっけ?><; 全く思い出せない><;」
みたいな感じ><
いわゆる歴史クラスタの人々が言うような「人の気持ちや時代背景を考えれば」みたいな必然性のない “導出” とはレベルが違うんですよね。「考えればわかる」のレベルの話をしている。
This account is not set to public on notestock.
This account is not set to public on notestock.
そもそもの話「わかる」は暗黙に「関連する事実が頭の中に入っているか、導出で引き出せる状態にある」ということでもあるので。特に数学のように合理的に「導出」ができる分野だと。
・・・・・それ、覚えてるとか暗記してるの範囲だとオレンジは思うんだけど><;
オレンジが言う「暗記できない><;」って、マジで本を掘りおこしてくるなりググるなりしなきゃわからないレベルの事なのであれかも><;
ここでいう「思い出す」は「記憶から掘り出せないので近隣の知識から導出する」を含みます
覚えておらずとも習ったことがあれば思い出せるし、そのくらいのことができないと大学での数学なんか到底追い付けないぞという話です
もし「数学の授業を暗記はできるけど、応用の要素が含まれると解けない」の方が通常の人間だとしたら、オレンジの物事の考え方ってまるっきり独特なやり方してるってことになるかも?><;
ていうか、オレンジが問題見る限りでは(いま48pまで見た)、これは数学の授業の内容を丸暗記していれば解ける問題群であり、かつ 覚えてなければ解けない問題に見えるけど、授業内容を暗記できててこれらを解けない人って、オレンジが想定する頭良い悪いの軸とは全然全く関係ない場所にいるんじゃないかってくらい「そんな人類いる!?><;」って感じに感じるし、どういうことなの?><;
あと、小さい頃に算数の宿題をMSX BASICで即席で専用計算器プログラムを作って解いて楽してた時の感覚がよみがえって来た><;
数学の問題を見た時にプログラミングで計算できる環境が無いと強烈なストレスを感じる感覚><
こう、方位磁針がないのに方位を訊ねられたみたいな焦燥感?みたいなやつ><
This account is not set to public on notestock.
某試験の某科目について「変にヒネった問題を出さず学校の知識で素直に解ける問題にしろ」的なのを見てしまって失笑を禁じえない
共通テスト2022 数学ⅠA問題|共通テスト解答速報2022|予備校の東進 https://www.toshin.com/kyotsutest/suugaku-1a_question_0.html
まともな数学教育を受けていないオレンジがやったら何点くらいなんだろう?><;(暗記しておかなきゃならない公式は小学生レベルのしか覚えてないから超低い?><;)
This account is not set to public on notestock.
ビジネス特集 お金の価値が1年で半分に減った国 | NHKニュース https://www3.nhk.or.jp/news/html/20220117/k10013434461000.html

This account is not set to public on notestock.
This account is not set to public on notestock.
This account is not set to public on notestock.
これもう誤差ってレベルじゃねえがwwwwww
>> ビールに換算すると83リットル~2万リットルと大量に摂取する必要がある
ビールが筋肉老化抑制 毎日83リットル飲めば: 日本経済新聞
https://www.nikkei.com/article/DGXNASDG2000O_Q2A920C1000000