ぶっこわれているいない(知識が欠落していない)なんて言ってないし、頂点側からたどっていかなければ必要な範囲の知識がどういった範囲かもわからないでしょ?><
って言ってる><
ボトムアップ式に基礎からやらなきゃわからないと言ってるならば、なぜ古文を学ばずに古文の知識が不要だといえるのか?><
ぶっこわれているいない(知識が欠落していない)なんて言ってないし、頂点側からたどっていかなければ必要な範囲の知識がどういった範囲かもわからないでしょ?><
って言ってる><
ボトムアップ式に基礎からやらなきゃわからないと言ってるならば、なぜ古文を学ばずに古文の知識が不要だといえるのか?><
「関係あるかどうかなんて無知な本人には判定しようがないんだから、パッケージをちゃんとやるかそれとも『穴開きでぶっ壊れていることを自覚して使う』か選ぶしかないだろ」という話で、そこに「穴開きかどうかなんて知らんが俺のはぶっ壊れてない!」と言われても、はあそうですかとしか言えませんよ。そう思うんならそうなんでしょう (ry
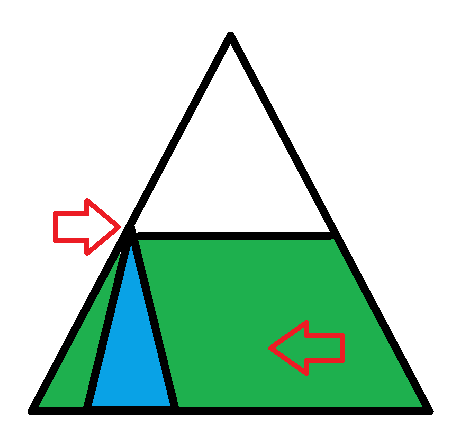
さっきの図で言うと、左の矢印が今回の文章を書く為にそろった知識の頂点、右の矢印が古文みたいな感じ><
他の人のたとえを借りるならなんで、古文を通る『登山道』ではなく『最短距離』を行ったのか?><
オレンジはもちろん左の矢印に至る為には緑の部分がすべて必要なんて思っていないので古文の知識は不要だと思ってるよ><
古文に見えるなら申し訳ありませんね、私は生きた日本語として書いているし普通に口頭で言うこともありますよ
その愉快な文章は、日本語での文章作成に関して大学辺りまで文学に関しても含めて学んだうえで書いたのでしょうか?><
それこそ要不要が取りざたされてる古文なんかも含めて><
Q: 「オチだけピックアップして読まずに全編いちいち読むようなことをやっていたら、どうやって読みたい本すべてを読めるというのか?」
A: 「もちろんすべて読めようはずもないが、そもそもオチをピックアップして話をわかったつもりになるのは本を読んだことにはならない。逆になんで『どうにか工夫すれば読みたい本すべてを読める』などという都合の良い仮定を無邪気に信じられるんだ?」
みたいな話
https://mstdn.nere9.help/@orange_in_space/112302772916679720
これでいうような緑の部分まで全部やるべきって考え方で、どうやって広範囲に興味を持ってむしろ非実用的な範囲まで学ぶのか?><
ある目的地を目指した登山であればもちろんそうでしょ><
そうではなく周辺の景色を楽しみたければその通りのルートを通って登ればいい><
非整数次元での距離の定義なんていう、一般的には何に使うんだかさっぱりわからない(オレンジもわからない><)ものに興味を持つ時点で、遠回りどころか寄り道しまくりの学習というかなんというかな感じだと思うけど><
「非整数次元での距離の定義なんてなにが面白いんだ?」って考え方の方がよほど最短距離的な考え方だと思うけど><
このアカウントは、notestockで公開設定になっていません。
自由化・制度改革で先行した英国が抱える課題
低炭素化と安定供給確保のため、市場メカニズムを修正
電力中央研究所 社会経済研究所 上席研究員 丸山 真弘
[pdf] https://criepi.denken.or.jp/koho/journal/eneco/2013/004.pdf
”1947 年に実施された電力国有化...”
"...1987 年 6 月の総選挙に大勝した
サッチャー政権は、1988 年 11 月に電力民営化法案を議会に提出した。
成立した電力法は1990 年 3 月 31日
に施行され、..."
6. 電気事業体制 - 英国の電気事業 | 電気事業連合会
https://www.fepc.or.jp/library/kaigai/kaigai_jigyo/britain/detail/1231572_4785.html
"英国では、1990年に、電力自由化と同時に国有電気事業者の分割・民営化が実施された。それまで発電と送電を独占していた国有の発送電局(CEGB)は発電会社3社と送電会社1社に分割・民営化された。また独占供給を行っていた12の国有配電局も民営化され配電会社となった。"
このアカウントは、notestockで公開設定になっていません。
このアカウントは、notestockで公開設定になっていません。
このアカウントは、notestockで公開設定になっていません。
目的からピラミッド状に分野を絞って勉強する場合と、そうではなくすべてを基礎から学んだ場合に必要な勉強量を、モデルを変えて比率みたいなのをその計算で出せるんじゃないの?><
って思った><
任意の大きさの任意の角度の二等辺三角形の内側に、それよりは小さい二等辺三角形が入ってる図形で、
内側の三角形の面積になる、外側の三角形をカットして台形にする高さって、公式にすればあれかも?><
2022年06月04日にスラドにこういうコメント書いたけど、
https://srad.jp/comment/4262313
リプのリプで答え書いてる人がいた><
https://srad.jp/comment/4262492
そこらへんでプログラミングに三角関数を使ってる人は、当然こんなの常識的に知ってたんだろうね><
オレンジは数学を基礎から学ばなかったから知らなかったけど、みんな基礎から数学を学んで、三角関数も学校でちゃんと学んだんでしょ?><
これ知ってグラフ出力した時マジでびっくりしたからね><
何年もかけてわかんなかったのに、あきらめてみた答えが予想以上にシンプルだったから><
https://mstdn.nere9.help/@orange_in_space/112246159926344131
https://mstdn.nere9.help/users/orange_in_space/statuses/112250144675201026
オレンジの思い違いで「いやいや、高校で数学を学べば、三角関数のちゃんとした定義とその定義に基づいた計算方法までセットで学んでいることは当たり前です」だったらあれだけど><
思い違いじゃなければそれこそ本当に基礎からやらないままで終わらせてスカスカだよね>< 学校教育としての数学><
学校教育での数学も、例えば三角関数に関して、それのちゃんとした定義をなぜか大学までちゃんとやらないしそれ自体を計算する方法も教えないの、それこそスカスカな教え方だと思うけど><
"興味がない (そもそも知らなかったことや辿り着けなかった未知の領域も含む) は何であれ「知っておくべき」の範疇に含まれない、という世界観なんですよね。説明はつくと思う。私はそういう世界観で見ていないけど。"
じゃあなんで非整数次元が数学の世界でどう扱われているかについて知らないの?><
少なくともChatGPTは、答えがあってるかは知らんけど、『それに関して簡単には説明するの難しいけど、詳しく知りたいのであればこの分野について学ぶとわかりますよ😊 』
って(実際に顔文字付きで)答えてくれるので「そうなんだ><」ってその分野について調べられるし、さらにそこでわかんなくて聞けば「詳しく知りたければこの分野を😊」って、どんどん何を学べばいいのか教えてくれる><
「基礎からやれ」に何の情報があるのか?><
図にした><
水色の三角のてっぺんが目的の知識だとして、オレンジが必要だと思ってるのは水色の部分、基礎からやれっていう話は緑と水色の両方><
だからくだらないと言ってる><
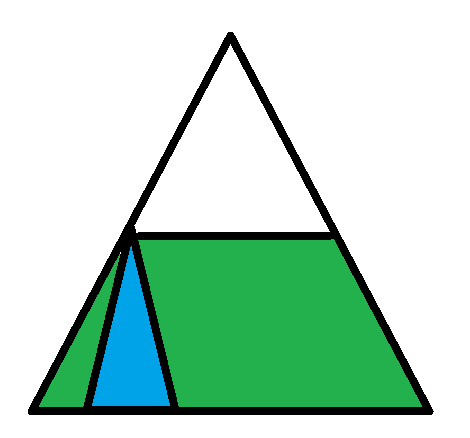
何らかの知識をピラミッド状/ツリー状に見立てたときに、ピラミッドのある石の位置の知識に必要なのは、その石を支えている石とさらにそれを支えている石の...であって、支えていないものも含めた低レベルにある全ての石ではない><
"そもそも空間に「穴をあける」ならそのための準備はできてるんか? というところが何も感じとれないんですが、たとえば座標系とかどう引くんです?"(以下略)
こういうのこそオレンジが言う、まるで『ない』かのような、数学の世界でも未定義かの言い方そのものかも><
数学ではどう扱われているか知りたいって話なのになぜオレンジが定義する話になるのか?><
(鍵エアリプ)
だから非整数次元に関するちゃんとした数学の世界では穴はどう扱われているのかという事自体が知りたい事なのに、なんでオレンジが定義する話になるのか?><#
ちなみにこの疑問は、メタに『自称数学好きな人がオレンジの疑問に対して『ない』と安易に答える現象』そのものから出発しています><
もっと単純に言うと、穴があいてる次元に於いての距離を、高次元からでは無く、その次元から見るとどうなるのか?><
シェルピンスキーのカーペットに限った話じゃなくむしろ今日初めて「よく考えたらシェルピンスキーのカーペットで考えたら自分でも計算できる可能性がある程度には単純なんじゃね?><」と思い至った><
https://mstdn.nere9.help/@orange_in_space/107567836363210148
2022年1月5日 12:55
"非整数次元(ハウスドルフ次元)のユークリッド距離ってどうなるんだろう?><
そもそもあるのか無いのか?><"
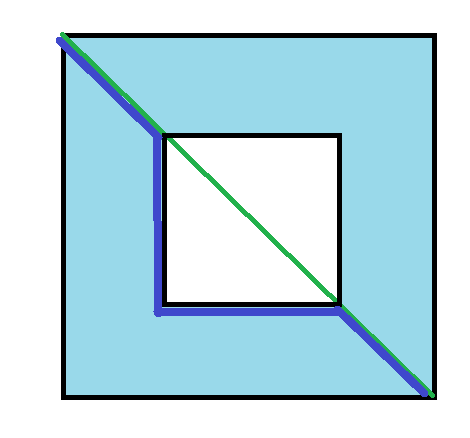
オレンジは真ん中の穴を空間の歪みが極端になったようなもので、穴に沿った部分が対角線になるのでは?><
って解釈で、この線で言うと青、シェルピンスキーのカーペットで言うと辺の長さの2倍に近づいていくって考えた><
でも、ChatGPTさんの解釈では真ん中の穴は空間の歪みではないですって解釈だった><
https://mstdn.nere9.help/@orange_in_space/107567836363210148
オレンジ元々書いた疑問がこれ><
つまり、フラットランドと同じ発想で、こういう穴が開いた四角の次元があった場合に、対角線である緑の線は『穴が開いた四角の次元の住人』から見てどう見えるか?><
高次元から見なければ穴の存在には気づけない><
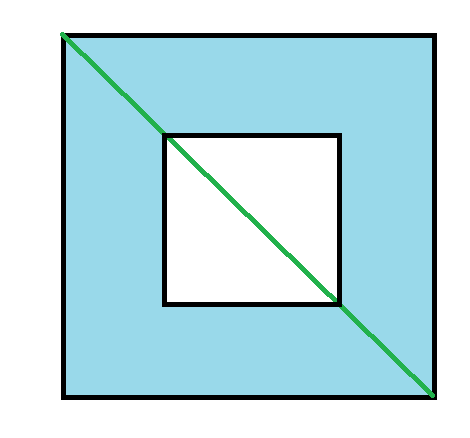
数学の一部ではあるけど、宇宙論に近い話になるっぽい?><
「オレンジ的には、フラットランドの考え方を穴が開いた次元にまで拡張するとどうなるか?><」が知りたかった><
穴がある空間の次元における対角線、つまり対角線も取り去られてしまうようなフラクタル空間の対角線は、高次元で見れば取り去られる前と同じだけど、同じ次元で見るとわけがわからないことになる?><;
なにがなんだかわからなくなったので、もっと単純化してフラクタルじゃなくして、シェルピンスキーのカーペットの第一段階、つまり、正方形の真ん中が1/3の辺の長さの正方形が取り去られただけの状態で、「その次元の生き物が居たらいろいろな現象がどういう風に見えるか?><」ってChatGPTさんと議論しまくったけど、
「穴がある次元の空間は、より高次元の中にしか存在できないので、結果的に穴がない空間から観察した結果になりそう」みたいな感じになった><
何回もChatGPTに聞いたら「無限だよ」「ゼロだよ」「2よりは大きいよ」「2よりはちいさいよ」「場合によって違うよ(???><;)」ってなってもうわけがわからなくなってきた・・・・><
同じようなツッコミを書くか迷ってたけど、オレンジが書いたらまたなぜかオレンジが間違ってることにされそうと思って書かなかった><
SDGsに対して「人類が滅びればSDGsを達成できるのでは」という皮肉があるが、SDGsの理念が1ミリも伝わっておらず、講義の感想に書いたら「私はほとんど寝てました」レベルで何も分かっていないということになる。
距離が負にもなる変な空間、空間(時空?)の中で時間が正にも負にもなる変な空間(時空?)であれば成り立つ・・・?><
そもそもシェルピンスキーのカーペットで対角線距離って言い方が正しいのか、それとも「対角の最短距離」みたいな言い方に変えなければいけないのかはまだわかんないけど><
オレンジ「フラクタル次元での対角線距離ってどうなるんだろ?><;」
らりおさん「そのもやっとした『距離』をされなきゃ話題にもならないだろ」
ChatGPT「ミンコフスキー距離を使ってp-ノルムの考え方で解く方法があるかもしれません」
で、ChatGPTさんのおかげで、少なくともシェルピンスキーのカーペットに関しては対角線距離はマンハッタン距離に収束するって事までたどり着けた><
オレンジは当たって砕けて「なんもわからん><」からの「わかるためには何を調べればいいんだろ?><」で勉強するみたいな感じの事を繰り返す感じの事をずっとしてきたけど><
じゃないとどうやって存在も知らない分野まで学ぶのさ?><
存在すら知らないままなら学びようもない><
オレンジが今おもしろがって調べてる疑問の話題だって、ミンコフスキー距離という言葉すらも知らないところから出発してるけど、この疑問を「どうせ高度だし無理だろう」ってあきらめてたらその言葉すら知らないままだった><
このアカウントは、notestockで公開設定になっていません。
オレンジは「この物質はこうだ!」なんて書かなかったし、実験できる環境も持ってないし、磁石に対して何も詳しくないけど、でも関連する報道を追ったり、論文を機械翻訳で読んで「なんもわからん><」ってしたりしてたけど、別に「この物質は絶対こうだ!」なんて決めつけしなくても「おもしろそう><」は書けるじゃん?><
自分にはそれ以上の掘り下げをできない「何だろうね」を呟くことを不毛だと思って黙っていただけの人もいるかもしれないのに?
資料を当たってみて「これは読んでもわからんな」と思って詳細について口を噤むことにした人もいるかもしれないのに?
「何だろう」を表明しないと「『だけ』で済ませてた」ことになっちゃうんです?
結論的なのが書いてある記事><(もっと詳しい記事があった気がするけど見つけられなかった><)
「常温常圧の超伝導体」として科学界に旋風を巻き起こしたLK-99が超伝導体ではないことはどのように明らかになったのか? - GIGAZINE
https://gigazine.net/news/20230817-lk-99-not-superconductor/

ちょっとずれるけど、韓国の自称常温常圧超伝導体「LK-99」の話題の時に、結構多くの人が「そんなわけないだろアホか」『だけ』で済ませてたじゃん?><
オレンジは、そうではなく「どう考えても常温超電導ではないだろうけど、この追試すると出来上がるヘンテコな磁石は何だろう?><」に興味示しまくってたじゃん?><
「科学的な視点ってどっちなんだろうね!><」ってすごく強くお思ってた><
さておき、 TL に思考を垂れ流してレベル近い同志いねーかな〜とぼやくのは普通に皆やってるのでそれはそれでいいと思うんですが、まあそうそういないものだし、場合によっては信念食い違ってる場合も結構あるので、それは普通に人間そういうものだし多様性ってそういうことなんじゃないですか
べつにおじさんでなくとも、おばさんとかおねーさんとかおにーさんとか爺婆でも何でもいいんですが。
世の中には「永久機関を作ったと自信満々に主張し続けるおじさん」とか「趣味でミレニアム問題を問いたと主張するおじさん」とか「対角線論法は嘘だと啓蒙し続けるおじさん」みたいなのがいて、「ああはなるまい」と自分を抑制している人はめちゃくちゃ多いと思いますよ。
つまり体系的でない学習によってちょっと視野が拡がったり知識がついたからといって、自分が識者に相当すると考えることへの抵抗は強いだろうし、「対角線論法は嘘だ!」と叫ぶような真似はすまいと思っている人はきっと多い。
内輪でというのはべつに秘密会合をしろと言っているわけではなく (オープンにしたければすればいい) 「恒常的に参加するメンバーはある程度既知または固定になるようにする、それ以外からの参加も監視も一切期待しない」くらいの非常に緩い意味です
もうこれはどう「他意はない」と言ったところで他意を読み取られてしまうだろうからそれを覚悟で言うけど、基礎なしにどんどん応用したがっちゃう人の好奇心につきあうのってめちゃくちゃ労力かかるし完全に工数と予算が必要な案件なんで、そのへんにいる random person に期待するのは完全に間違っていると思いますね。独りでやるかどうにかして同志を探して内輪でやるべき
話飛ぶけど、ChatGPTに数学関連の質問する時のメモ帳として、数学好きのおばけの人が作ったこれすごく便利><
draft.hyuki.net: 数式まじりのメモを書くためのシンプルなWebアプリ - 結城浩の数学ノート
https://math.hyuki.net/20180513233343/

このアカウントは、notestockで公開設定になっていません。
このアカウントは、notestockで公開設定になっていません。
自称数学好きって少なくとも高校数学辺りまではついていけた人々だろうから、オレンジよりも頭よさそうだけど・・・><
このアカウントは、notestockで公開設定になっていません。
このアカウントは、notestockで公開設定になっていません。
オレンジは色んな分野に対して「なにそれ知らなかったし考えたこともなかったおもしろそう!><」って反応しまくってるじゃん?><
オレンジは超多趣味だからいろいろな分野にそうなるけど、数学が趣味なり数学が好きなのであれば、数学の話題に限ってはそういう反応が起こらないの?><
って謎><
反応だけで言ったらオレンジの方が数学好きじゃん?><
数学界隈にそういう事に興味を示す人を全然観測できないから「数学嫌い><」だけど><
このアカウントは、notestockで公開設定になっていません。
オレンジのフラクタル次元での距離に関する疑問も「ねーよそんなもん」されてる気分だしそのことを言ってるんだけど><
このアカウントは、notestockで公開設定になっていません。
これって数学ではないの?><
型理論 - Wikipedia
https://ja.wikipedia.org/wiki/%E5%9E%8B%E7%90%86%E8%AB%96

型云々で言うならば「数学に型ってないの?><」「ねーよそんなもん! 数学の世界は純粋なんだよ!」からの「型って数学の集合論のやつなんじゃん!><# 嘘つき!><# 」は実際にあった><
たとえがなんか違う気がする><
「こういう考え方(パラダイム)のプログラミング言語ってないのかな?」に対して「ねーよそんなもんアホか」って言われたけど、探したらマイナーな言語だけどあるんじゃんってなるみたいな感じ><
つまり型の話をしてるのに Haskell 使ってなくてコンパイラ書いたこともないやつは全員にわかでしょーもない連中ってこと? それならわかる
そういうことを言ってるんじゃなくて、おもしろがる人が少なくない?>< って言いたいし、オレンジの観測範囲に現れる自称数学好きが、実は高度な問題だったりするものを「ねーよ」で済ます人が多すぎるって言ってる><
このアカウントは、notestockで公開設定になっていません。
このGPTが示したシェルピンスキーのカーペットの対角線距離の式、
d_{\text{sierpinski}} = \lim_{{n \to \infty}} \frac{{\sqrt{n}}}{3^n}
あってるかそもそもわからないけど、知ってた人って居たの?><
あるいはこれが明確に間違ってると説明できる人って居るの?><
「ねーよそんなもん」って思ってた人ばかりなんじゃないの?><
で、フラクタル次元に対角線距離はあるの?><
昨日まで無いかもしれないと思ってたしググっても見つからないから自分で考えようってなったけど、GPTさんに式をどうしたらそれっぽく書けるか質問してたらこんなことが起きたけど><
https://mstdn.nere9.help/@orange_in_space/112301159653446305

しかも、「ねーよそんなもん」からの「そうなの?><;」からの「あるんじゃん!><# 嘘つき!><# 」ばかり繰り返されてるから、自称数学好きの「ねーよそんなもん」は基本的にあてにならないと思ってる><
べつに自分で歩くのは結構なんですが、「飛行機を面白がってばかりで発明・製作しようとしないやつらはつまらん」みたいなこと言われても知るか俺の勝手だろ勝手に作って勝手に墜落してろとなりません?
ならんか。まあそういう人もいよう。
言っちゃ悪いけど、私だって自分のわかる分野でテキトー言ってる人がいたら「基礎からやりなおせ」とだけ思って見なかったことにしたりしますよ。べつに関心をひかなかったすべての事例がそれに該当しているなどと言うつもりは毛頭ないけど。
だったら謎の「フラクタル次元での距離」を組み立てるために必要な条件は何かって所から出発するのが本来の数学好きというか、数学を組み立ててきた人が行ってきたことじゃないの?><
「ググったけどなかったはw つまり無い」とどっこいどっこいの事をするのが数学なの?><
これは全く適当話でしかないんですが、概念の定義ってやつをちゃんと勉強すると「この条件がないとこういう不都合があるからこれが必要」みたいなある種の反駁を事前にやるものなので、それを経てない人のいう「面白い」は既知だったりするんじゃないですか。
具体例を何一つ持ってないので適当話ですが。
数学好きを自称してる中で目立つやつらを見て「つまんないな><」って思ってるのはそういう所だよ><
どうやったら組み立てられるかって数学の歴史で起きてきたプロセスの延長を行うんじゃなく、すでに行われた結果だけ見てるようなのばかりで、だから「数学ってつまらないし嫌い><」ってオレンジは自称してるんだよ><
その各々バラバラのぼんやりをぼんやりじゃなくてちゃんと定義しようって作られたのがユークリッド幾何学とかじゃないの?><
各々の脳内にしか無いっぽいなら、どうやったらちゃんと定義が作れるのかって考えて組み立てることこそが数学の歴史じゃないの?><
なんかわからんけど内的にぼんやり持っているイメージを明文化したいみたいやモチベーションならわかるけど、その言語化はぼんやりを内的に持っている人自身がやるしかないわけで……他の人はそのぼんやりの中に複数のはっきりとした別々のものを見ているかもしれない (そして「どれのことだよ」と。)
昨晩のオレンジの「もしノルムを拡張して負のノルムを作って、負の距離なるものがある変な空間がるとしたらどんな空間になるのか?><;」とかも、「そんなのねーよ」じゃなくて、「どんなおかしなことになるのか?」って考えるの楽しいでしょ?><
って数学好きな人々はならないの?><
そこに興味を何で持たないのか?>< って話><
「そもそも穴が開いてるフラクタル次元での距離ってなんだろう?><;」って面白い話題でしょ?><
って言いたい><
定義されていない幻のツチノコの話をされても、そりゃ誰も参加できるわけなくない?
"会話をしたいわけではない「感想をリプライでぶら下げる」"は、「RT/BT後の言及でいいじゃん?><;」ってなるけど、知らん人から話しかけられるのは別に嫌じゃなくてむしろ色々な人の意見が聞けておもしろい派なオレンジ><
会話をしたいわけではない「感想をリプライでぶら下げる」と、「知らん人から話しかけられるのが嫌」の世代が被っているイメージがあって、世代間というわけでもないんだろうなと思ったが、その人が過ごしてきた経験なのか、よくわからん。
オレンジは数学嫌いなのに、この話題すごくおもしろいと思うのに、"シェルピンスキーのカーペットの対角線距離"でググっても引用符ありだと一件も出てこないし、これをおもしろい話題と思ってる日本語圏の数学好きはいないっぽさ><
ChatGPTさんにそれ以外の点の間違いを尋ねたら、まずオレンジが「無限に近づく」って考えたのは間違いまたは用語の間違いで、実際には「収束する」で、あと、対角線をとって代わりに対応する辺を割り当てるって考えるのは(結果的には同じ値になっても)フラクタル次元の理解の面では単純化しすぎてるらしい・・・><
シェルピンスキーのカーペットの対角線距離って、結局のところ、対角線から対角線の一部を切り抜いて対応する辺の一部を足していく操作を無限に行うことになるので、
同じ大きさの正方形の対角線の距離であるユークリッド距離から、同じ大きさの正方形の辺の長さの2倍、つまり、マンハッタン距離に無限に近づく事になる><
p-ノルムで言うと、少なくとも全体の対角線においては、pを2から1に無限に近づけていくのが正方形をシェルピンスキーのカーペットにしていくことなのかも><(あってるかわからん)
C# で書いたシェルピンスキーのカーペットの対角線距離の計算プログラムこれ><
これやってみて「なんで2に近づいていくの?><」ってなってぐるぐる考えて「そういうことか!!!!!><;」ってなった><
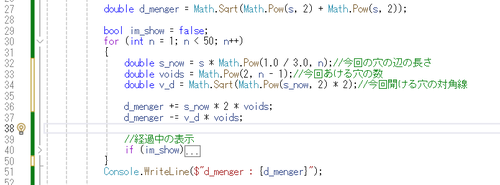
シェルピンスキーのスポンジの対角線距離の公式、C# で実際に計算しながら思い至って、それをGPT4さんに式にしてもらおうとしたら、こんな事になった><

ちょっとググってもそのものズバリの計算式が出てこなかったけど、もしもマジで誰も(そんなものに興味が無くて)作ってないならオレンジが発見者(?)になれるのかも?><;
GPT3.5(4と違って数学に関してあんまり頭よくなくて珍回答多い)とおしゃべりしててふと思ったけど、フラクタル図形の対角線距離の計算は一般的に高度で難しいっぽいけど、シェルピンスキーのスポンジであれば構造が単純なので、オレンジが対角線距離を計算する公式を作り出せるんでは?><