昨日のマストドンの活動は
トゥート : 4326(+40)
フォロー : 38(0)
フォロワー : 47(0)
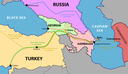
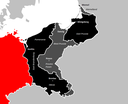
ボリビアの名目上の首都はラパスじゃないらしい
名目上の首都と実質的な首都が違うのオランダしか知らなかった
タンザニアもらしい
https://ja.wikipedia.org/wiki/ダルエスサラーム
https://ja.wikipedia.org/wiki/%E7%90%B5%E7%90%B6%E6%B9%96#%E8%87%AA%E7%84%B6%E5%8F%B2
琵琶湖が古代湖なの意外
ほかの古代湖(世界で20ほど)を見てみるとフィリピンもあるし、億単位の古さのものはないから湖って相当なくなりやすいものなんだろうな(恒常的に蒸発するし)
年齢のソートがうまく行ってない気がする
https://ja.wikipedia.org/wiki/古代湖
Template:出典無効 - Wikipedia https://ja.wikipedia.org/wiki/Template:%E5%87%BA%E5%85%B8%E7%84%A1%E5%8A%B9
あんまりGoogle検索でもヒットしなかった
毎年数百はある模様
> 方法としての集合論
数学の公理系というのは絶対のものではなく，それによって数学的対象を定義する．逆に言えば，数学的現象，数学的真理を記述する方法である．集合論の公理も数学の方法であり，基礎の方法として，数学の言葉である．
方法に絶対のものはなく，数学の発展とともに，方法もまた変化し発展する．今日の数学の新たな枠組みを作ったフランスを中心とする数学者集団ブルバキは，このことを端的に次のように述べる．
もし，未来にそれ(現在の数学の枠組みとなっている公理的集合論)が破綻しても数学は必ずや新しい基礎を見つけるだろう．
体系とは完結したものではなく，それ自体が開かれた発展する方法なのである．このような立場からいえば，解析の基礎を考え学ぶうえでは，このような矛盾の存在をおさえつつ，とりあえず素朴な集合論からはじめればよい．
http://aozoragakuen.sakura.ne.jp/kaisekikiso/node9.html
所有者がBPでん？となったがNATOのトルコとバクーをつないでるので当然冷戦終結後でそこにBPがからんでいるのもなんらおかしないことだった
