what's tricky is numbers go on forever.
1, 2, 3, 4, … is only the beginning.
large numbers beyond graham's number are still "natural numbers".

(ultrafinitists deny the existence of numbers that are too large.)

note commutativity, distributivity etc can be proved by a method called induction (other than using lego).

philosophically, there can be 2 ways of thinking:
• numbers are such code in reality
• no, such code are just a miniature model of numbers

i stand with the former,
but on 2nd thought the latter may be more rational.

sounds like there's a kinda programming language within math.
numbers can be programmed/coded with it.

there could also be implementations on a computer, such as Lean.

just as atoms are made of elementary particles, it seems that numbers can be made from sets, functions (church encoding), or categories (or topoi).

as sets:
0 = {}
1 = {{}}
2 = {{}, {{}}}
3 = {{}, {{}}, {{}, {{}}}}

there's a definition of numbers called
• Peano axioms.
i haven't figured it out yet.

when we ask smtg like "why does 1+1=2?", it is said that we face the so-called
• Münchhausen trilemma.

marbles, number lines, or areas of figures can be used as well.
i suspect one aspect of these is the "unary numeral system".

like
3 + 4
= 111 + 1111
= 1111111
= 7.

cr: https://www.resolve.edu.au/algebra-odds-and-evens https://commons.wikimedia.org/wiki/File:Square_number_16_as_sum_of_gnomons.svg

Lego bricks can be used for visualizing numbers.

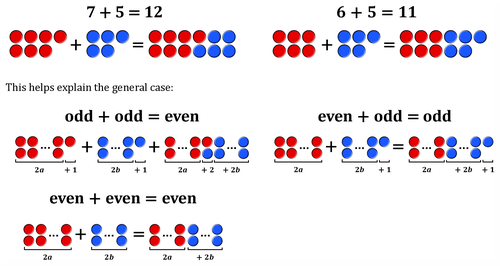
parity arithmetic:
even + even = even
even + odd = odd
odd + odd = even

sum of odd numbers:
1 + 3 + 5 + … + (2n - 1) = n²

it has limitations and it's hard to believe that lego is the nature of numbers.

• What are numbers?
i mean,
• What is the nature of natural numbers?

Conclusion: it's hard.

it's a fundamental question, but not an easy one to answer.
it's better to pretend to know such "obvious" things and move on.

0:00 js woke up.
same breakfast every day.
coffee, persimmon, muesli, yogurt