霜降り明星のラジオのちんちんの言い方のくだりでいつも笑ってる
訳あって3歳下のいとこ（女の子）がうちに1週間泊まることになったが、部屋が足りないので俺の部屋で寝ることになってほしい
\frac {\partial} {\partial y} f(x(y,z),y,z) \\
= \frac {\partial} {\partial x} f(x(y,z),y,z)
\frac {\partial x} {\partial y}
+ \frac {\partial} {\partial y} f(x(y,z),y,z)
？？？？？？
@carbontwelve@mstdn.jp あーーー、なるほど
右辺第2項ではxが固定できてるのか
じゃあ
∂f(x,y,z)/∂y と ∂f(x(y,z),y,z)/∂y
の二つの書き方では結果が変わるってことでいいの
@sr@mstdn.mell0w-5phere.net
g(y,z) = f(x(y,z), y, z) だけど、 ∂g/∂y ≠ ∂f/∂y になるということか
右辺の偏微分の場合xの中身のyまで固定されてるからか
@sr@mstdn.mell0w-5phere.net なるほど
x(y,z) と書くのと単に x と書くのとでは意味が変わるのね
@sr@mstdn.mell0w-5phere.net あーめっちゃすっきりするね
その感じで提出する！ありがと
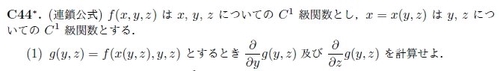
@sr@mstdn.mell0w-5phere.net 2つの「ここで」の行でΔの極限とらずに偏導関数がでてきてるけどそれは記述上OKなの
「正論がいつも正しい訳じゃないんだよ」というやつ、単に「正論を言わない方がいい場合もある」と言えばいいのにパラドキシカルなこと言いたがるからこじれる
@mametsuko@co.misskey.io 読んでる間はちゃんと理解してるんだけどねえ、あつこさんレベルでもそうか
@mametsuko@co.misskey.io あーわかる、やっぱり日本語の形で頭の中に既にある知識とか理屈とのくっつきが弱い感じする
